Las ciencias formales al detalle: disciplinas y enfoques
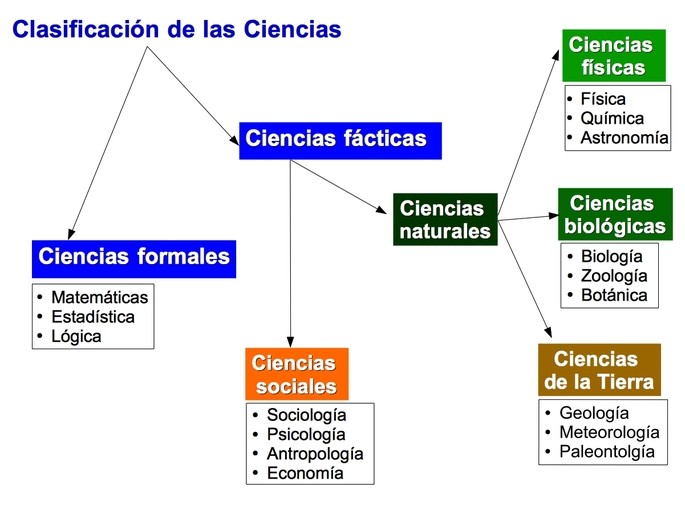
Las ciencias formales son aquellas que se encargan del estudio de los sistemas lógicos y matemáticos, y se diferencian de las ciencias naturales en que no se basan en la observación empírica del mundo físico. A continuación, vamos a detallar las principales disciplinas y enfoques de las ciencias formales.
Lógica
La lógica es la disciplina que se encarga del estudio de la inferencia y el razonamiento, y se divide en dos áreas principales: la lógica proposicional y la lógica de predicados. La lógica proposicional se ocupa del estudio de las proposiciones y sus conectores lógicos, mientras que la lógica de predicados se ocupa del estudio de las relaciones entre objetos y las propiedades que tienen.
Teoría de conjuntos
La teoría de conjuntos es la disciplina que se encarga del estudio de los conjuntos, sus propiedades y sus relaciones. Esta disciplina es fundamental en la matemática moderna y ha sido utilizada para desarrollar gran parte de la teoría matemática de la actualidad.
Teoría de números
La teoría de números es la disciplina que se encarga del estudio de los números enteros y sus propiedades. Esta disciplina es fundamental en la criptografía y en la teoría de códigos, y ha sido utilizada para desarrollar algoritmos de gran importancia para la seguridad de la información.
Álgebra abstracta
El álgebra abstracta es la disciplina que se encarga del estudio de las estructuras algebraicas, como los grupos, los anillos y los campos. Esta disciplina es fundamental en la teoría de la computación y en la teoría de códigos, y ha sido utilizada para desarrollar algoritmos de gran importancia para la criptografía y la seguridad de la información.
Teoría de la computación
La teoría de la computación es la disciplina que se encarga del estudio de los fundamentos matemáticos de la informática. Esta disciplina se enfoca en el estudio de los lenguajes formales, la complejidad computacional, la teoría de autómatas y la teoría de la recursividad.
Geometría
La geometría es la disciplina que se encarga del estudio de las figuras geométricas y sus propiedades. Esta disciplina es fundamental en la física y la ingeniería, y ha sido utilizada para desarrollar algoritmos de gran importancia para la computación gráfica y la realidad virtual.
Análisis matemático
El análisis matemático es la disciplina que se encarga del estudio de las funciones, las derivadas, las integrales y las ecuaciones diferenciales. Esta disciplina es fundamental en la física y la ingeniería, y ha sido utilizada para desarrollar algoritmos de gran importancia para la simulación y el modelado.
Enfoque axiomático
El enfoque axiomático es un enfoque que se basa en la formulación de axiomas y la deducción de teoremas a partir de ellos. Este enfoque es fundamental en la matemática moderna y ha sido utilizado para desarrollar gran parte de la teoría matemática de la actualidad.
Enfoque constructivista
El enfoque constructivista es un enfoque que se basa en la construcción de objetos matemáticos a partir de objetos más simples. Este enfoque es fundamental en la teoría de la computación y ha sido utilizado para desarrollar algoritmos de gran importancia para la simulación y el modelado.
Enfoque lógico
El enfoque lógico es un enfoque que se basa en el uso de la lógica para el estudio de los sistemas matemáticos. Este enfoque es fundamental en la teoría de la computación y ha sido utilizado para desarrollar algoritmos de gran importancia para la criptografía y la seguridad de la información.
Enfoque algebraico
El enfoque algebraico es un enfoque que se basa en el uso del álgebra para el estudio de los sistemas matemáticos. Este enfoque es fundamental en la teoría de la computación y ha sido utilizado para desarrollar algoritmos de gran importancia para la criptografía y la seguridad de la información.
Enfoque analítico
El enfoque analítico es un enfoque que se basa en el uso del análisis matemático para el estudio de los sistemas matemáticos. Este enfoque es fundamental en la física y la ingeniería, y ha sido utilizado para desarrollar algoritmos de gran importancia para la simulación y el modelado.
Enfoque geométrico
El enfoque geométrico es un enfoque que se basa en el uso de la geometría para el estudio de los sistemas matemáticos. Este enfoque es fundamental en la física y la ingeniería, y ha sido utilizado para desarrollar algoritmos de gran importancia para la computación gráfica y la realidad virtual.
Enfoque probabilístico
El enfoque probabilístico es un enfoque que se basa en el uso de la teoría de la probabilidad para el estudio de los sistemas matemáticos. Este enfoque es fundamental en la estadística y la teoría de la información, y ha sido utilizado para desarrollar algoritmos de gran importancia para la inteligencia artificial y el aprendizaje automático.
Conclusión
Las ciencias formales son fundamentales para la comprensión y el desarrollo de la matemática y la informática. Cada disciplina y enfoque tiene su propia importancia y aplicación en diferentes áreas de la ciencia y la tecnología.
Preguntas frecuentes
¿Por qué son importantes las ciencias formales?
Las ciencias formales son importantes porque proporcionan los fundamentos matemáticos y lógicos necesarios para la comprensión y el desarrollo de la ciencia y la tecnología modernas.
¿Qué es la lógica?
La lógica es la disciplina que se encarga del estudio de la inferencia y el razonamiento.
¿Qué es la teoría de conjuntos?
La teoría de conjuntos es la disciplina que se encarga del estudio de los conjuntos, sus propiedades y sus relaciones.
¿Qué es la teoría de números?
La teoría de números es la disciplina que se encarga del estudio de los números enteros y sus propiedades.
¿Qué es la álgebra abstracta?
El álgebra abstracta es la disciplina que se encarga del estudio de las estructuras algebraicas, como los grupos, los anillos y los campos.
¿Qué es la teoría de la computación?
La teoría de la computación es la disciplina que se encarga del estudio de los fundamentos matemáticos de la informática.
¿Qué es la geometría?
La geometría es la disciplina que se encarga del estudio de las figuras geométricas y sus propiedades.
¿Qué es el análisis matemático?
El análisis matemático es la disciplina que se encarga del estudio de las funciones, las derivadas, las integrales y las ecuaciones diferenciales.

Deja una respuesta