Puntuación Z de 1,96: ¿Qué significa y cómo interpretarla?

Si alguna vez has oído hablar de la puntuación Z, probablemente te hayas preguntado qué significa y cómo interpretarla. La puntuación Z es una medida estadística que se utiliza para comparar las puntuaciones de una muestra con una población de referencia. Una puntuación Z de 1,96 es un valor bastante común, pero ¿qué significa exactamente?

¿Qué es la puntuación Z?

Antes de profundizar en la puntuación Z de 1,96, es importante entender qué es la puntuación Z en sí misma. La puntuación Z es una medida estadística que indica cuántas desviaciones estándar se encuentra una puntuación de una muestra con respecto a la media de una población de referencia.

En otras palabras, si una puntuación tiene una puntuación Z de 1, esto significa que está una desviación estándar por encima de la media de la población de referencia. Una puntuación Z de -1 significaría que la puntuación está una desviación estándar por debajo de la media.

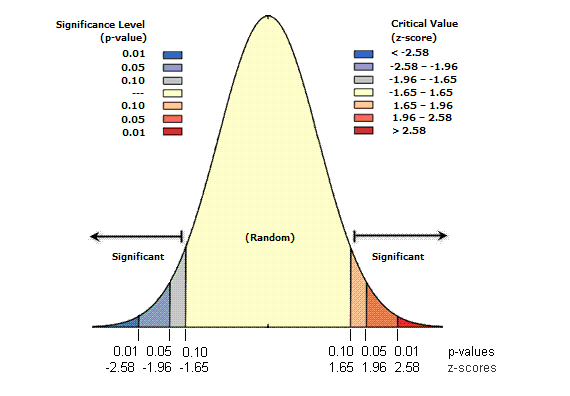
¿Qué significa una puntuación Z de 1,96?

Una puntuación Z de 1,96 es una medida estadística que indica que una puntuación se encuentra a 1,96 desviaciones estándar por encima de la media de la población de referencia. En términos prácticos, esto significa que la puntuación es relativamente alta en comparación con la población de referencia.

En el contexto de la investigación, una puntuación Z de 1,96 puede ser utilizada para determinar si los resultados de una muestra son estadísticamente significativos. Si la puntuación Z es igual o superior a 1,96, se considera que los resultados son estadísticamente significativos.

¿Cómo interpretar una puntuación Z de 1,96?

Interpretar una puntuación Z de 1,96 depende en gran medida del contexto en el que se utiliza. En el contexto de la investigación, una puntuación Z de 1,96 indica que los resultados son estadísticamente significativos. Esto significa que hay una alta probabilidad de que los resultados no sean el resultado del azar.

En el contexto de las pruebas estandarizadas, una puntuación Z de 1,96 también puede ser útil para interpretar los resultados. Por ejemplo, si un estudiante obtiene una puntuación Z de 1,96 en una prueba, esto significa que su puntuación está por encima del promedio de la población de referencia en dos desviaciones estándar.

¿Cómo se calcula la puntuación Z?

La fórmula para calcular la puntuación Z es bastante sencilla. Primero, se resta la media de la población de referencia de la puntuación de la muestra. Luego, se divide el resultado por la desviación estándar de la población de referencia.

La fórmula completa es:

Z = (X - μ) / σ

Donde:

Z = puntuación Z
X = puntuación de la muestra
μ = media de la población de referencia
σ = desviación estándar de la población de referencia

¿Por qué es importante la puntuación Z?

La puntuación Z es una medida estadística importante porque permite comparar las puntuaciones de una muestra con la población de referencia. Esto es particularmente útil en la investigación, ya que permite determinar si los resultados son estadísticamente significativos.

En el contexto de las pruebas estandarizadas, la puntuación Z también es importante porque permite comparar las puntuaciones de los estudiantes con la población de referencia. Esto permite evaluar el rendimiento de los estudiantes en comparación con otros estudiantes.

Conclusión

La puntuación Z es una medida estadística importante que se utiliza para comparar las puntuaciones de una muestra con la población de referencia. Una puntuación Z de 1,96 indica que una puntuación se encuentra a 1,96 desviaciones estándar por encima de la media de la población de referencia. Esto puede ser utilizado para determinar si los resultados de una muestra son estadísticamente significativos.

Preguntas frecuentes

1. ¿Qué es una desviación estándar?

La desviación estándar es una medida estadística que indica cuánto se desvían las puntuaciones de una muestra de la media.

2. ¿Cómo se interpreta una puntuación Z negativa?

Una puntuación Z negativa indica que una puntuación se encuentra por debajo de la media de la población de referencia.

3. ¿Qué es una muestra?

Una muestra es un conjunto de datos que se utiliza para representar una población más grande.

4. ¿Qué es una población de referencia?

Una población de referencia es un conjunto de datos que se utiliza como base para comparar las puntuaciones de una muestra.

5. ¿Para qué se utiliza la puntuación Z en la investigación?

La puntuación Z se utiliza en la investigación para determinar si los resultados de una muestra son estadísticamente significativos.

6. ¿Qué significa una puntuación Z de 0?

Una puntuación Z de 0 indica que una puntuación es igual a la media de la población de referencia.

7. ¿Por qué es importante interpretar la puntuación Z correctamente?

Es importante interpretar la puntuación Z correctamente porque puede afectar la interpretación de los resultados de la muestra y la toma de decisiones basadas en esos resultados.